Basic Concepts of Rotational Motion
Basic Concepts of Rotational Motion: Overview
This topic covers concepts, such as, Motion of a Rigid Body, Rigid Body, Relative Angular Velocity & Relative Angular Acceleration etc.
Important Questions on Basic Concepts of Rotational Motion
Angular position of a line of a disc of radius is given by . The average angular speed (in ) between is:
Find the maximum height upto which disc can reach on the incline plane when given velocity horizontally and disc is performing pure rolling motion.
. A coin placed on a revolving disc, with its centre at a distance offrom the axis of rotation just slips off when the speed of the revolving disc exceeds. What should be the maximum angular speed of the disc, so that when the coin is at a distance of from the axis of rotation, it does not slip?
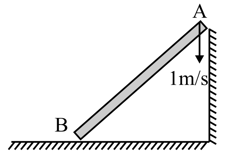
A rod of length is sliding in a corner as shown. At an instant when the rod makes an angle of with the horizontal plane, the velocity of point on the rod is . The angular velocity of the rod at this instant is:
the angular speed of earth around the Sun is
A horizontal heavy uniform bar of weight is supported at its ends by two men. At the instant, one of the men lets go off his end of the rod, the other feels the force on his hand changed to:
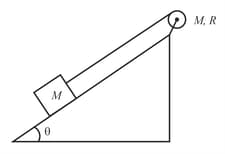
A block of mass is released from rest on top of a smooth inclined plane of inclination. The block is connected to a light string which is wound over a disc shaped pulley of mass and radius as shown. If length of inclined surface is , then time (in second) taken by the block to reach the bottom is-------------------(given:)
When a ceiling fan is switched off, its angular velocity reduces to of its initial value while it makes rotations. If angular retardation of the
fan is uniform, then how many more rotations will it make before coming to rest?
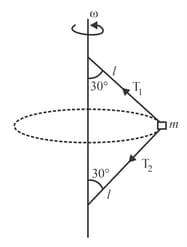
A particle of mass is whirled in horizontal circle with the help of two threads of length each as shown in figure. Angular velocity equals , then
A block of mass fastened to the end of a steel wire of unstretched length , is whirled in a vertical circle with angular velocity of . The cross- sectional area of wire is . The elongation of wire when mass is at lowest point of its path is [Where is Young's modulus of steel wire]
The equation for angular displacement of a particle, moving in a circular path (radius) is given by: where is the angular displacement at the end of. Find (i) angular velocity and acceleration at start, (ii) time when the particle reaches its maximum angular velocity, and(iii) maximum angular velocity of the particle.
A force . is applied on a block, whose position is . The block moves on a circular path of radius . Find the work done by the force in a complete rotation.
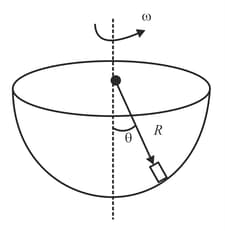
A hollow hemispherical bowl having radius of inner smooth surface is rotated with angular velocity = . A small object is placed at rest w.r.t. the bowl of position as shown. Find angle .
At an instant velocity of a particle is and its acceleration is .Find radius of curvature of the path of particle at this instant.
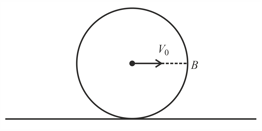
A disc of radius is rolling without slipping with velocity on a stationary surface. The radius of curvature of path of particle B at the position shown is B
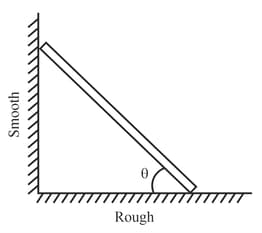
One end of a uniform rod rests against a smooth vertical wall and other end on rough horizontal floor. If coefficient of friction between the lower end of rod and floor is , then minimum angle of inclination of rod with horizontal, can be
The speed of a particle in a circle is along the circumference of a circle of radius If the speed increases at the rate of . The acceleration of the particle at a given instant is
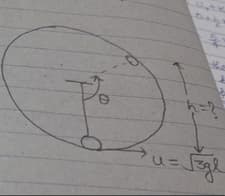
Find the height at which the string becomes slack
Four point size metal spheres each of mass are placed on a turn table and are connected by four strings of equal length to form a square. If the spheres are rotated with an angular frequency , the tension in the connecting strings is
